* 본 포스트는 개인연구/학습 기록 용도로 작성되고 있습니다.
[Python] 평균-분산 포트폴리오 전략
By MK on January 27, 2019
포트폴리오 이론은 해리 마코위츠에 의해 체계화된 이론으로, 자산을 분산투자하여 포트폴리오를 만들게 되면 분산투자 전보다 위험을 감소시킬 수 있다는 이론이다.
자산의 가치는 미래의 기대수익률과 위험의 두 요소에 의해 결정 되며 미래의 기대수익률이 클수록 그리고 위험이 작을수록 자산의 가치는 높아진다. 위험회피형 투자자는 두 투자안의 기대수익률이 동일하다면 표준편차가 작은 투자안을 선택할 것이다.
즉 투자안의 수익률의 표준편차가 동일하다면 기대수익률이 상대적으로 큰 투자안을 선택할 것이다. 이를 평균-분산 혹은 지배원리 라고 한다.
포트폴리오들 중에서 동일한 위험을 지녔으나 기대수익이 높거나, 동일한 기대수익을 가져다 주지만 위험이 낮은 포트폴리오는 그렇지 않은 포트폴리오를 지배한다. 이러한 지배원리를 통해 서로 지배할 수 없는 포트폴리오들의 조합을 효율적투자선이라고 한다.
사용한 라이브러리
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.neighbors import KDTree
from pandas.plotting import scatter_matrix
from scipy.spatial import ConvexHull
from datetime import datetime
np.random.seed(0)
[참고] 한글출력
import matplotlib.font_manager as fm
font_fname = 'C:/Windows/Fonts/HYNAMM.TTF'
font_family = fm.FontProperties(fname=font_fname).get_name()
plt.rcParams["font.family"] = font_family
1. 데이터 가져오기
def stock_reader(kospi_df, code_list, df='p', n=0):
if n == 0:
n = len(code_list)
stock_df = pd.DataFrame()
stock_df['Date'] = kospi_df['Date']
print("동기간 KOSPI 생성일수 : ", len(kospi_df['Date']))
normal_cnt = 0
err_cnt = 0
code_nm_list = []
symbol_list = []
for code in code_list:
stock = df_krx[df_krx.Symbol == code]
code_nm = list(stock.Name)[0]
symbol = list(stock.Symbol)[0]
try:
temp = fdr.DataReader(code, strt_dt, end_dt)
# 데이터일수가 시장보다 작으면 skip(최근 상장 데이터로 판단)
if len(temp) < len(kospi_df['Date']):
err_cnt += 1
print("skip : (",err_cnt,")", code, code_nm, strt_dt, end_dt, ", 건수 : ", len(temp))
continue
temp.reset_index(inplace = True)
temp_df = pd.merge(temp[['Date','Close', 'Open']], kospi_df[['Date']], on='Date', how='right')
if df == 'v':
stock_df[code_nm] = temp_df.Close - temp_df.Open #variation
elif df == 'p':
stock_df[code_nm] = temp_df.Close # price
normal_cnt += 1
code_nm_list.append(code_nm)
symbol_list.append(symbol)
print("정상 : (",normal_cnt,")", code, code_nm, strt_dt, end_dt, ", 건수 : ", len(temp), "->", len(stock_df))
except:
err_cnt += 1
print("skip : (",err_cnt,")", code, code_nm, strt_dt, end_dt, ", 건수 : ", len(temp))
if normal_cnt == n:
print('총', n,'개 생성 설정 / ', normal_cnt, '개 생성 완료')
break # n개 종목 생성시 종료
# 데이터 정렬
stock_df.sort_values('Date', ascending=True, inplace=True) # ascending=True 오름차순, False 내림차순
# 결측치 채우기
stock_df.fillna(method='ffill', inplace=True)
return stock_df, code_nm_list, symbol_list
n = 5 # 생성할 종목수 지정
df_krx_list = df_krx['Symbol'].head(n*2) # 임시로 2배까지 루프
stock_df, code_nm_list, symbol_list = stock_reader(kospi_df, df_krx_list, 'p', n) # v :variation, p : price(close)
stock_df.dropna(inplace=True)
data = stock_df.set_index('Date')
2. 종목별 상관계수
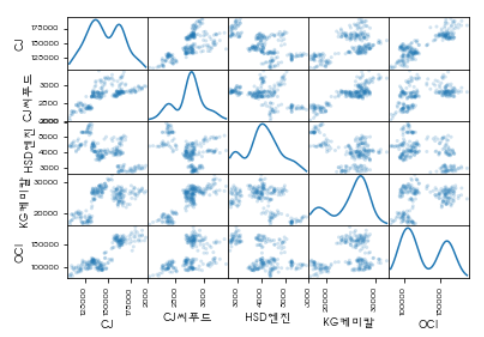
scatter_matrix(data, alpha=0.2, diagonal='kde')
plt.show()
종목관 상관도를 확인할 수 있다.
CJ와 CJ씨푸드는 우상향으로 상관도가 높으며(1에 가까움),
CJ와 HSD엔진은 우하향하며 상관도가 낮음(-1에 가까움)을 확인할 수 있다.
3. 포트폴리오 설정
현재 포트폴리오를 임의로 설정해보자.
종목별 Weight 설정
# 현재 포트폴리오 설정 (랜덤 Weight로 산출)
num_assets = np.size(code_nm_list)
cur_value = (1e4-5e3)*np.random.rand(num_assets,1) + 5e3
tot_value = np.sum(cur_value)
weights = cur_value.ravel()/float(tot_value)
weights를 출력해보면 다음과 같다.
array([0.13952466, 0.25070935, 0.18619368, 0.25026474, 0.17330757])
포트폴리오 리스크 설정
#compute portfolio risk
Sigma = data.cov().values
Corr = data.corr().values
volatility = np.sqrt(np.dot(weights.T, np.dot(Sigma, weights)))
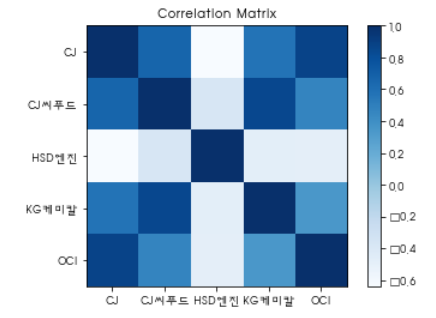
4. 종목별 상관관계 메트릭스
plt.figure()
plt.title('Correlation Matrix')
plt.imshow(Corr, cmap=plt.cm.Blues)
plt.xticks(range(len(code_nm_list)),data.columns)
plt.yticks(range(len(code_nm_list)),data.columns)
plt.colorbar()
plt.show()
5. 시뮬레이션
무작위 Weight 조정으로 시뮬레이션을 반복 수행한다.
# 각 자산의 평균 가격을 기준으로 무작위 Weight를 지정한다.
num_trials = 1000
W = np.random.rand(num_trials, np.size(weights))
W = W/np.sum(W,axis=1).reshape(num_trials,1) #normalize
pv = np.zeros(num_trials) #portoflio value w'v
ps = np.zeros(num_trials) #portfolio sigma: sqrt(w'Sw)
avg_price = data.mean().values
adj_price = avg_price
for i in range(num_trials):
pv[i] = np.sum(adj_price * W[i,:])
ps[i] = np.sqrt(np.dot(W[i,:].T, np.dot(Sigma, W[i,:])))
points = np.vstack((ps,pv)).T
hull = ConvexHull(points)
plt.figure()
plt.scatter(ps, pv, marker='o', color='b', linewidth = '3.0', label = 'tangent portfolio')
plt.scatter(volatility, np.sum(adj_price * weights), marker = 's', color = 'r', linewidth = '3.0', label = 'current')
plt.plot(points[hull.vertices,0], points[hull.vertices,1], linewidth = '2.0')
plt.title('expected return vs volatility')
plt.ylabel('expected price')
plt.xlabel('portfolio std dev')
plt.legend()
plt.grid(True)
plt.show()
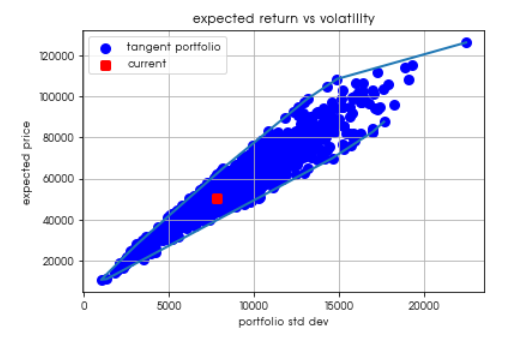
무작위로 생성된 포트폴리오는 아래와 같다.
가로는 위험, 세로는 포트폴리오 가치를 나타낸다. 우상향할수록 위험과 가치가 모두 큰 것을 의미한다.
위험은 낮으면서 수익이 큰 것이 선호된다. 단, 위험을 허용할 수 있는 효용성이 다르며 이에 따른 최적 포트폴리오(효율적 프론티어)는 허용하는 위험하에 최대 수익을 낼수 있는 곡선 상단에 있는 포트폴리오 세트로 정의된다.
무위험자산을 추가함으로써 Sharpe 비율로 정의된 기울기를 가진 접선을 따라 만나는 지점에서 포트폴리오를 선택할 수 있다.
현재 위치로 표시되는 붉은 지점의 좌표를 확인 한 뒤, 인근 K개의 포트폴리오를 선택해보자!
대략 현재 포트폴리오가 어떤 범주에서 움직일 수 있을지 가늠이 가능하다.
knn = 5
kdt = KDTree(points)
query_point = np.array([80000, 60000]).reshape(1,-1) # 위 그래프에서 현재 포인트(red)를 지정한다.
kdt_dist, kdt_idx = kdt.query(query_point,k=knn)
print("top-%d closest to query portfolios:" %knn)
print("values: ", pv[kdt_idx.ravel()])
print("sigmas: ", ps[kdt_idx.ravel()])
top-5 closest to query portfolios:
values: [69912.88333592 75806.36415751 74547.52730116 69736.22594794
78656.57351551]
sigmas: [14649.86852454 15713.1785078 15279.90167408 14208.52745236
15971.61030831]
Reference
https://github.com/vsmolyakov/fin/blob/master/portfolio_opt.py