* 본 포스트는 개인연구/학습 기록 용도로 작성되고 있습니다.
[Python] Inverse Covariance를 통한 수익률 유사도 측정
By MK on January 27, 2019
공분산(covariance)은 정밀도(precision)와 역의 관계에 있다. 분산이 무한대 인 경우 정밀도는 0이 되며 반대로, 분산이 0 일 때, 무한 정밀도를 갖는다.
즉 역공분산은 (Inverse covariance)은 정밀도(precision)를 의미한다.
역공분산은 종속성의 그래프 네트워크를 구성하는 데 유용하게 쓰일 수 있다.
여기서는 일일 Open 가격과 Close 가격의 차이를 사용하여 희소정밀도(sparse precision) 행렬을 추정하기 위해 그래프 lasso algorithm에 맞는 경험적 공분산(empirical covariance)을 사용한다.
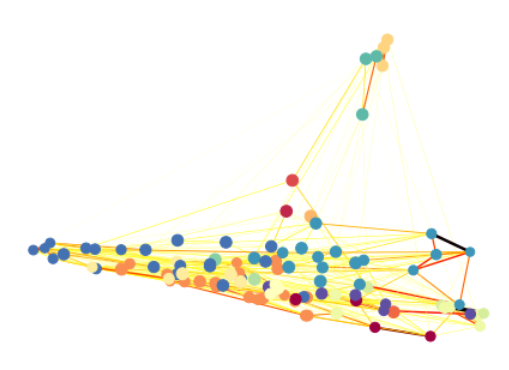
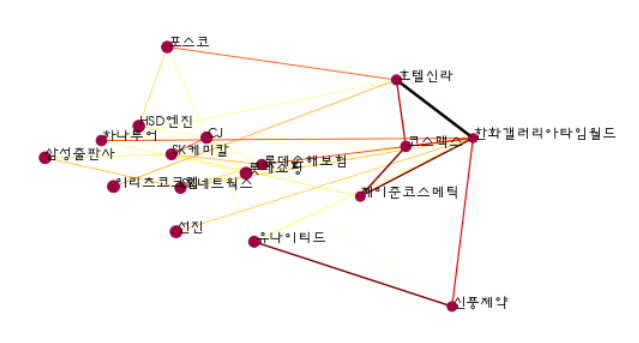
종목별 결과는 아래와 같이 표현될 수 있다.
point들은 각 개별 종목이며 유사 그룹은 색상으로 표시된다. 눈에 잘 띄지는 않지만 연결 강도는 선의 진하기로 나타낼수 있다.
다시 정리하자면,
종목들간의 유사도를 측정하여 클러스터링하고, 각각의 연결 강도를 측정하며 공간상의 위치를 나타내게 되는데 그 방법론은 아래와 같다.
- 일일 가격변화 표준값 X = (Close - Open) / std
- 클러스터링 그룹(labels) : X의 공분산값을 기준으로 음의 제곱 유클리드 거리 계산, (GraphLassoCV, affinity_propagation)
- 종목의 위치(embedding) : 일별 가격변동의 표준화값을 기준으로 2차원 embedding (LocallyLinearEmbedding)
- 연결강도(partial_corr) : X의 정밀도값을 기준으로 결정(그룹내에서 실제 유사도가 얼마나 큰지) (GraphLassoCV)
정밀도의 의미상의 개념은 유사하다고 측정된 그룹에서 실제 얼마나 관련이 있는지의 정도 를 나타낸다.
단, 데이터 기간 설정시 너무 길면 정밀도가 매우 낮게 나온다.
사용한 라이브러리
import FinanceDataReader as fdr
fdr.__version__
import numpy as np
import pandas as pd
from scipy import linalg
from datetime import datetime
import pytz
from sklearn.datasets import make_sparse_spd_matrix
from sklearn.covariance import GraphLassoCV, ledoit_wolf
from sklearn.preprocessing import StandardScaler
from sklearn import cluster, manifold
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection
np.random.seed(0)
1. 데이터 가져오기
종목별 일자별 Close, Open 가격 데이터가 필요하다.
아래 코드는 FinanceDataReader를 사용할때 특정 기간내 종목별 데이터 건수가 상이하여 임시 작업한 케이스이다.
기간은 반기로 설정하였다.
# 한국거래소 상장종목 전체
# 용도 : 코드와 종목명 가져오기
df_krx = fdr.StockListing('KRX')
# 코스피 종목 추출
# 용도 : DataReader 사용시 종목별 기간 조회 건수가 상이하다.
# 코스피 데이터 날짜를 기준으로 가져오기 위해 사용
strt_dt = '2018-07-01' # 시작일 지정
end_dt = '2018-12-31' # 종료일 지정
kospi_df = fdr.DataReader('KS11', strt_dt,end_dt)
kospi_df.reset_index(inplace = True)
이전 포스팅 함수에서 파라메터를 추가하여,
df 옵션에 따라 v이면 variation = close-open, p이면 close를 추출할 수 있도록 하였다.
def stock_reader(kospi_df, code_list, df='p', n=0):
if n == 0:
n = len(code_list)
stock_df = pd.DataFrame()
stock_df['Date'] = kospi_df['Date']
print("동기간 KOSPI 생성일수 : ", len(kospi_df['Date']))
normal_cnt = 0
err_cnt = 0
code_nm_list = []
symbol_list = []
for code in code_list:
stock = df_krx[df_krx.Symbol == code]
code_nm = list(stock.Name)[0]
symbol = list(stock.Symbol)[0]
try:
temp = fdr.DataReader(code, strt_dt, end_dt)
# 데이터일수가 시장보다 작으면 skip(최근 상장 데이터로 판단)
if len(temp) < len(kospi_df['Date']):
err_cnt += 1
print("skip : (",err_cnt,")", code, code_nm, strt_dt, end_dt, ", 건수 : ", len(temp))
continue
temp.reset_index(inplace = True)
temp_df = pd.merge(temp[['Date','Close', 'Open']], kospi_df[['Date']], on='Date', how='right')
if df == 'v':
stock_df[code_nm] = temp_df.Close - temp_df.Open #variation
elif df == 'p':
stock_df[code_nm] = temp_df.Close # price
normal_cnt += 1
code_nm_list.append(code_nm)
symbol_list.append(symbol)
print("정상 : (",normal_cnt,")", code, code_nm, strt_dt, end_dt, ", 건수 : ", len(temp), "->", len(stock_df))
except:
err_cnt += 1
print("skip : (",err_cnt,")", code, code_nm, strt_dt, end_dt, ", 건수 : ", len(temp))
if normal_cnt == n:
print('총', n,'개 생성 설정 / ', normal_cnt, '개 생성 완료')
break # n개 종목 생성시 종료
# 데이터 정렬
stock_df.sort_values('Date', ascending=True, inplace=True) # ascending=True 오름차순, False 내림차순
# 결측치 채우기
stock_df.fillna(method='ffill', inplace=True)
return stock_df, code_nm_list, symbol_list
n = 100 # 생성할 종목수 지정
df_krx_list = df_krx['Symbol'].head(n*2) # 임시로 2배까지 루프
stock_df, code_nm_list, symbol_list = stock_reader(kospi_df, df_krx_list, 'v', n) # v :variation, p : price(close)
동기간 KOSPI 생성일수 : 123
정상 : ( 1 ) 001040 CJ 2018-07-01 2018-12-31 , 건수 : 136 -> 123
정상 : ( 2 ) 011150 CJ씨푸드 2018-07-01 2018-12-31 , 건수 : 128 -> 123
정상 : ( 3 ) 082740 HSD엔진 2018-07-01 2018-12-31 , 건수 : 127 -> 123
정상 : ( 4 ) 001390 KG케미칼 2018-07-01 2018-12-31 , 건수 : 133 -> 123
정상 : ( 5 ) 010060 OCI 2018-07-01 2018-12-31 , 건수 : 145 -> 123
...
총 100 개 생성 설정 / 100 개 생성 완료
2. 일일 가격변동 표준화값 설정
stock_df.dropna(inplace=True)
X = stock_df.set_index('Date')
X /= X.std(axis=0) # 표준화
3. Inverse Covariance 측정
#estimate inverse covariance
graph = GraphLassoCV(verbose=10) # 그리드서치를 통해 유의한 alphas가 있는 경우 지정
graph.fit(X)
gl_cov = graph.covariance_
gl_prec = graph.precision_
gl_alphas =graph.cv_alphas_
gl_scores = np.mean(graph.grid_scores, axis=1)
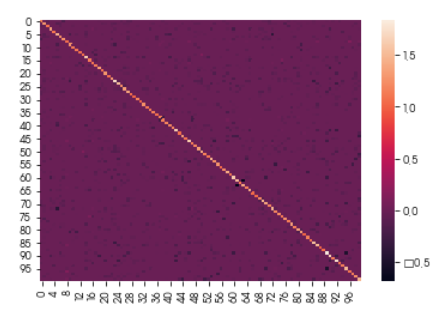
plt.figure()
sns.heatmap(gl_prec) # vmin=-2, vmax=2
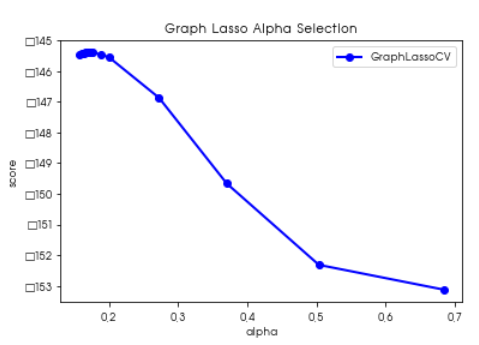
alpha 선택을 위한 그리드서치
plt.figure()
plt.plot(gl_alphas, gl_scores, marker='o', color='b', lw=2.0, label='GraphLassoCV')
plt.title("Graph Lasso Alpha Selection")
plt.xlabel("alpha")
plt.ylabel("score")
plt.legend()
4. 종목 클러스터링
affinity_propagations는 음의 제곱 유클리드 거리를 통해 유사도를 측정 한다.
유사도 s(i,k) 는 아래와 같이 표현된다.
| s(i,k) = − | xi−xk | 2 |
s(k,k)는 특정한 음수 값으로 사용자가 정해주게 되는데 이 값에 따라서 클러스터의 갯수가 달라지는 하이퍼 모수가 된다. s(k,k)가 크면 자기 자신에 대한 유사도가 커져서 클러스터의 수가 증가한다.
기본 설정이 인수(preference)로 전달되지 않으면 입력 유사성의 중앙값으로 설정됩니다.
더 이상 변화하지 않고 수렴하면 계산이 종료되고 종료 시점에서 r(k,k)+a(k,k) > 0이 데이터가 클러스터의 중심이 된다.
names = np.array(code_nm_list)
symbols = np.array(symbol_list)
#cluster using affinity propagation
_, labels = cluster.affinity_propagation(gl_cov) # 공분산 데이터로 클러스터링
num_labels = np.max(labels)
for i in range(num_labels+1):
print("Cluster %i: %s" %((i+1), ', '.join(names[labels==i])))
Cluster 1: SH에너지화학, 삼영전자공업, 삼영화학공업, 코오롱플라스틱
Cluster 2: STX
Cluster 3: 고려제강
Cluster 4: 골든브릿지증권
Cluster 5: CJ씨푸드, OCI, WISCOM, 갤럭시아에스엠, 극동유화, 대영포장, 대유에이텍, 대한해운, 동국실업, 모두투어리츠, 삼성SDI, 아시아나항공, 영화금속, 인지컨트롤스, 조일알미늄, 키다리스튜디오, 태양금속공업, 한국주철관공업, 한국철강, 한솔테크닉스
Cluster 6: 롯데하이마트
Cluster 7: 삼성카드, 삼성화재해상보험, 신한지주
Cluster 8: KG케미칼, 윌비스, 제주항공, 한국패러랠, 한진, 한창제지, GH신소재
Cluster 9: 유니온머티리얼, 코웨이, EG
Cluster 10: 경동도시가스, 노루페인트, 삼성바이오로직스, 삼진제약, 일동제약, 한미약품
Cluster 11: 동아쏘시오홀딩스, 제일약품, 제일파마홀딩스
Cluster 12: 조흥
Cluster 13: 지역난방공사
Cluster 14: 남양유업, 태광산업, 현대홈쇼핑
Cluster 15: CJ, HSD엔진, SK네트웍스, SK케미칼, 롯데손해보험, 롯데쇼핑, 삼성출판사, 선진, 신풍제약, 유나이티드, 이리츠코크렙, 제이준코스메틱, 코스맥스, 포스코, 하나투어, 한화갤러리아타임월드, 호텔신라
Cluster 16: 까뮤이앤씨, 대림씨엔에스, 대원제약, 동방, 동양, 마니커, 무림페이퍼, 미래에셋생명, 선도전기, 세이브존I&C, 우진, 제이에스코퍼레이션, 제일연마, 코오롱인더, 한국가스공사, 한세실업, 한일철강, 현대건설, 현대건설기계, 현대비앤지스틸, 호전실업, CJ프레시웨이
Cluster 17: 세원셀론텍, 웅진에너지, 원림, 진도, 코리아써키트, GST
5. 시각화를 위한 Embedding
그래프 표현을 위해 2차원([0],[1])으로 표현한다. 모든 주식간 지역적 위치를 계산한다.
node_model = manifold.LocallyLinearEmbedding(n_components=2, n_neighbors=6, eigen_solver='dense')
embedding = node_model.fit_transform(X.T).T # 일일 가격차 표준화값( (close-open)/std)을 기준으로 embedding
6. 특정 Group 이미지 출력
임의로 원하는 라벨을 지정해 해당 그룹의 관계를 파악해보자.
1) 원하는 그룹 데이터 추출
select_label = 14 # 라벨 사용자 지정
plot_temp = pd.DataFrame()
plot_temp['symbols'] = list(symbols)
plot_temp['names'] = list(names)
plot_temp['gl_prec'] = list(gl_prec)
plot_temp['em0'] = list(embedding[0])
plot_temp['em1'] = list(embedding[1])
plot_temp['labels'] = list(labels)
result_df = plot_temp
plot_temp = plot_temp[plot_temp['labels'] == select_label]
# 임베딩 변경
em0_array = plot_temp['em0']
em1_array = plot_temp['em1']
embedding_temp = np.vstack([em0_array, em1_array])
| symbols | names | gl_prec | em0 | em1 | labels |
|---|---|---|---|---|---|
| 001040 | CJ | [1.1631385235465022, -0.0, -0.0727619155778179… | 0.052146 | 0.020026 | 14 |
| 082740 | HSD엔진 | [-0.07276191557781794, -0.026297425600196038, … | 0.021124 | 0.026313 | 14 |
| 001740 | SK네트웍스 | [-0.0, -0.079680739004616, -0.0622622361779819… | 0.040177 | -0.007522 | 14 |
이하 데이터 생략
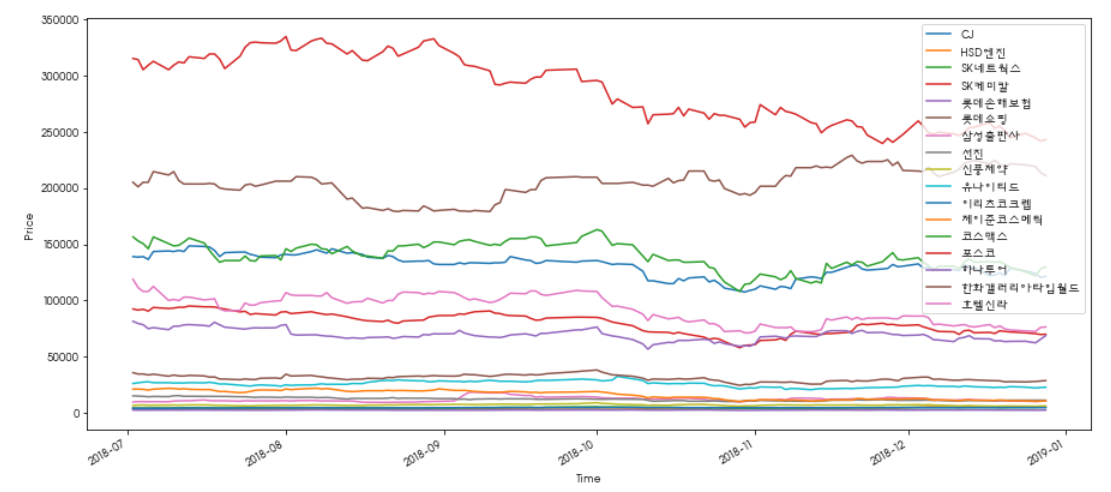
2) 종목별 시세움직임 비교하기
일일 종가가 어떻게 움직여 왔는지 파악해보자.
종가 가져오기
group_df, group_names, group_symbols = stock_reader(kospi_df, list(plot_temp['symbols']) , 'p', n) # v :variation, p : price(close)
group_df.set_index('Date', inplace=True)
그래프 그리기
group_df.plot(figsize=(15,7))
plt.ylabel('Price');
plt.xlabel('Time');
plt.show()
어느정도 유사한 패턴으로 움직이고 있는 것을 확인할 수 있다.
3) 그룹내 종목별 관계도 그래프
Precisiton 재설정
prec_temp = pd.DataFrame()
final_df = pd.DataFrame()
total_prec = ()
for x in range(0,len(plot_temp)):
prec_temp['gl_prec'] =list(plot_temp['gl_prec'].iloc[x])
prec_temp['labels'] = list(labels)
final_df = prec_temp[prec_temp['labels'] == select_label]
if len(total_prec) == 0:
total_prec = np.array(final_df['gl_prec'])
else:
total_prec = np.vstack([total_prec, np.array(final_df['gl_prec'])])
그래프 그리기
# 일일 가격변화 표준값 X = (Close - Open) / std
# 클러스터링 그룹(labels) : X의 공분산값을 기준으로 음의 제곱 유클리드 거리 계산, (GraphLassoCV, affinity_propagation)
# 종목의 위치(embedding) : 일별 가격변동의 표준화값을 기준으로 2차원 embedding (LocallyLinearEmbedding)
# 연결강도(partial_corr) : X의 정밀도값을 기준으로 결정(그룹내에서 실제 유사도가 얼마나 큰지) (GraphLassoCV)
plt.figure()
plt.clf()
ax = plt.axes([0.,0.,1.,1.])
plt.axis('off')
partial_corr = total_prec
d = 1 / np.sqrt(np.diag(partial_corr))
non_zero = (np.abs(np.triu(partial_corr, k=1)) > 0.02) #connectivity matrix
#plot the nodes
plt.scatter(plot_temp['em0'],plot_temp['em1'], s = 100*d**2, c = plot_temp['labels'], cmap = plt.cm.get_cmap("Spectral"))
#plot the edges
start_idx, end_idx = np.where(non_zero)
# segments = [[np.array(plot_temp['em0'].iloc[:start])[0], np.array(plot_temp['em1'].iloc[:stop])[0]] for start, stop in zip(start_idx, end_idx)]
segments = [[embedding_temp[:,start], embedding_temp[:,stop]] for start, stop in zip(start_idx, end_idx)]
values = np.abs(partial_corr[non_zero])
lc = LineCollection(segments, zorder=0, cmap=plt.cm.hot_r, norm=plt.Normalize(0,0.7*values.max()))
lc.set_array(values)
lc.set_linewidths(5*values)
ax.add_collection(lc)
#plot the labels
for index, (x_names, x_labels, (x,y)) in enumerate(zip(np.array(plot_temp['names']),np.array(plot_temp['labels']), np.array(plot_temp[['em0','em1']]))):
plt.text(x,y,x_names,size=12)
선의 색상은 정밀도를 통한 연결강도를 의미한다.
7. 분석대상 전체 그래프
#generate plots
plt.figure()
plt.clf()
ax = plt.axes([0.,0.,1.,1.])
plt.axis('off')
partial_corr = gl_prec
d = 1 / np.sqrt(np.diag(partial_corr))
non_zero = (np.abs(np.triu(partial_corr, k=1)) > 0.02) #connectivity matrix
#plot the nodes
plt.scatter(embedding[0], embedding[1], s = 100*d**2, c = labels, cmap = plt.cm.get_cmap("Spectral"))
#plot the edges
start_idx, end_idx = np.where(non_zero)
segments = [[embedding[:,start], embedding[:,stop]] for start, stop in zip(start_idx, end_idx)]
values = np.abs(partial_corr[non_zero])
lc = LineCollection(segments, zorder=0, cmap=plt.cm.hot_r, norm=plt.Normalize(0,0.7*values.max()))
lc.set_array(values)
lc.set_linewidths(5*values)
ax.add_collection(lc)
#plot the labels
# for index, (name, label, (x,y)) in enumerate(zip(names, labels, embedding.T)):
# plt.text(x,y,name,size=12)
편의상 종목명 라벨은 생략하였다.
Reference
https://github.com/vsmolyakov/fin/blob/master/inv_cov.py