* 본 포스트는 개인연구/학습 기록 용도로 작성되고 있습니다.
[Python] 공적분을 활용한 Pair Trading
By MK on January 25, 2019
공적분검정을 통해 개별주식간의 동조화 여부를 확인할 수 있다.
동조화는 추세가 공유되는 장기동조화와 순환이 이전되는 단기동조화로 분해된다.
비정상 시계열의 경우 추세의 공유 여부는 공적분 분석에 의해 수행된다. 순환의 이전은 오차수정 모형에서 차분변수의 그랜저인과관계 분석을 통해 수행한다.
특정 주식의 한 쌍이 동조화를 이룰때 주가의 차이 또는 비율의 차이를 스프레드라고 하며 이는 일정한 간격을 유지할 것으로 기대하게 된다.
하지만 특정 이슈로 일시적인 격차가 벌어지거나 좁혀졌을때, 이 현상이 시간에 따라 정상으로 회귀할 것으로 예측 된다면 Pair Trading이 가능하다.
Pair Trading에서 공적분 검증을 활용하는 기본 아이디어 를 정리하면 아래와 같다.
연관된 두 시계열의 공통 주세를 제거하고 남은 잔차 성분(스프레드)이 정상 시계열이면 두 시계열은 공적분 관계에 있다. 이 때 잔차 성분의 정상성을 최대로 만드는 비율을 공적분 계수로 활용할 수 있다.
단, 공적분의 의한 방법론은 주가가 비정상 시계열임을 가정하고 스프레드의 정상성을 추구한다.
1. 데이터 가져오기
import numpy as np
import pandas as pd
import statsmodels
from statsmodels.tsa.stattools import coint
import matplotlib.pyplot as plt
np.random.seed(42)
data = pd.read_csv('./datas/data_all.csv')
tickers = ['Shinhan', 'KB']
# 인덱스 설정
data.set_index('Date', inplace=True)
# 데이터 정렬
data.sort_values('Date', ascending=True, inplace=True) # ascending=True 오름차순, False 내림차순
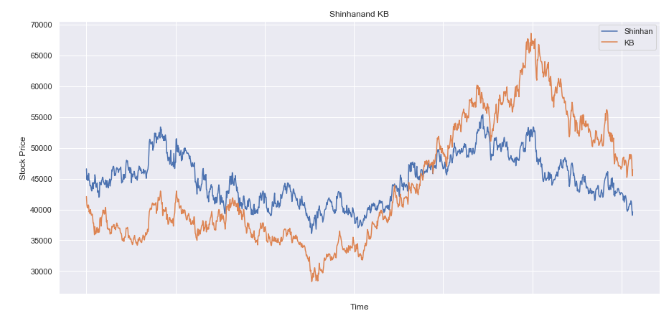
주가 추이 그래프
pd.concat([data[tickers[0]], data[tickers[1]]], axis=1).plot(figsize=(15,7))
plt.ylabel('Stock Price');
plt.xlabel('Time');
title = tickers[0] + 'and ' + tickers[1]
plt.title(title)
2. 공적분 분석 요소 셋팅
상관관계와 유사한 공적분은 두 주식간의 비율이 평균을 중심으로 달라짐을 의미한다. 요소항목은 log 처리한 종가를 사용하거나 단순 종가 혹은 일별 수익률을 사용하기도 한다.
두 주식 X, Y의 관계는 다음과 같이 정의 할 수 있다.
Y = ⍺ X + e
⍺는 일정한 비율이고 e는 백색 잡음이다.
Pair Trading이 가능하려면 시간 경과에 따른 비율의 기대값이 평균에 수렴해야 한다. 즉, 공적분 관계가 성립되어야 함을 의미한다.
공적분 관계 성립 조건
각각의 시계열들이 모두 같은 order of integration을 가진다. (order of integration이란 어떤 시계열이 정상적(stationary)이 되기 위해 필요한 차분(difference) 횟수를 말한다.) 시계열들의 선형 결합으로 만들어진 새로운 시계열은 기존의 시계열들보다 더 낮은 order of integration을 가진다.
공적분 쉽게 이해하기
공적분을 쉽게 설명하는 일화로 ‘취한 남편과 아내’, 혹은 ‘취한 사람과 그의 개’ 이야기가 있다. 아래에는 취한 사람과 개 이야기를 적어둔다. 어떤 취한 사람이 비틀거리며 어디론가 걷고 있다. 이 때 이 사람이 어디로 갈 지는 아무도 모른다. 다만 현재 자기가 있는 자리에서 어디론가 이동하려 한다는 것은 알 수 있다. 이것을 랜덤워크(random walk), 즉 무작위로 걷는다고 한다.(실제로 시계열분석시 볼 수 있는 통계용어다.) 만약 이런 취한 사람이 두 명 있다면 그들은 서로 각자 알아서 길을 갈 것이다. 즉 랜덤워크의 특성을 지닌 시계열이 두 개 있는 셈이다. 이 두 취한 사람들이 걸어간 자취 사이에는 아무 상관관계도 없다. 그런데, 이런 취한 사람 한 명이 애완견비글을 목줄 묶어서 데리고 다닌다고 생각해보자. 그렇다면 애완견이 이리저리 무작위로 뛰어다닌다 해도 결국 이 취한 사람이 가는 길과 비슷한 길을 가게 된다. 즉 애완견이 있는 위치와 취한 사람이 있는 위치 사이의 거리는 일정 수준 이상을 벗어나지 않는 다는 것을 알 수 있다. 이 때 애완견의 위치를 나타내는 시계열과 취한 사람의 위치를 나타내는 시계열은 공적분 관계에 있다고 할 수 있다.
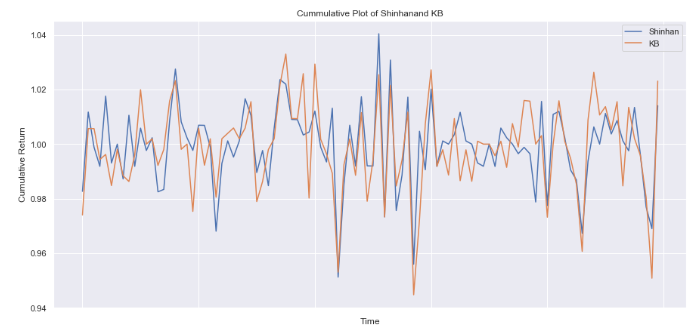
일일 수익률 계산
편의상 최근 100일치 데이터만 확인
cumm_rtn = (1 + data.pct_change()) # 일일수익률
cumm_rtn = cumm_rtn.dropna()
cumm_rtn = cumm_rtn.tail(100)
X = cumm_rtn.Shinhan
Y = cumm_rtn.KB
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.ylabel('Cumulative Return');
plt.xlabel('Time');
title = 'Cummulative Plot of ' + tickers[0] + 'and ' + tickers[1]
plt.title(title)
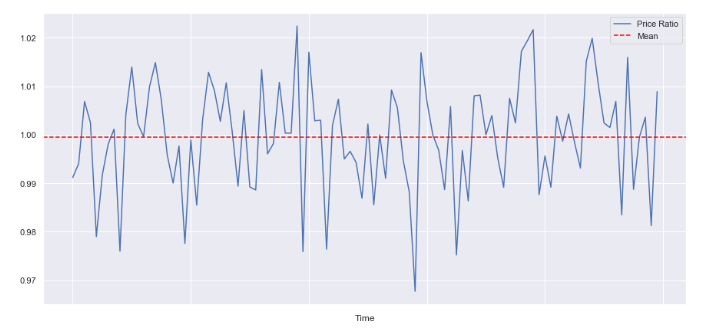
3. 공적분 계산
(Y/X).plot(figsize=(15,7))
plt.axhline((Y/X).mean(), color='red', linestyle='--')
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()
4. 공적분 검증
score, pvalue, _ = coint(X,Y)
print('Correlation: ' + str(X.corr(Y)))
print('Cointegration test p-value: ' + str(pvalue))
Correlation: 0.7454929874474863
Cointegration test p-value: 3.883901182423506e-0
공적분의 p-value가 매우 적게 나와 유의한 것으로 판정된다. 즉, 신한지주와 KB금융은 장기적으로 유의한 관계가 있다.
5. Pair Trading 활용
이제 다시 원점으로 돌아와, 이러한 유의한 2개의 쌍을 찾는 것 부터 시작해보자. 예시로 100개의 종목 데이터를 추출해왔다.
1) 데이터 가져오기
상장 종목별 시계열데이터를 생성해야 한다.
여기서는 FinanceDataReader 모듈을 사용했다.
다만, 종목별로 생성되어 있는 일자가 상이해 KOSPI 지수 데이터를 기준으로 삼고 종목별 시계열 데이터를 맞추고자 한다.
이에 따라, 잘 정비된 데이터를 사용한다면 스킵해도 되는 코드를 일부 포함하고 있다.
import FinanceDataReader as fdr
fdr.__version__
# 한국거래소 상장종목 전체
# 용도 : 코드와 종목명 가져오기
df_krx = fdr.StockListing('KRX')
df_krx.head()
| Symbol | Name | Sector | Industry | |
|---|---|---|---|---|
| 0 | 001040 | CJ | 기타 금융업 | 지주회사 |
| 1 | 011150 | CJ씨푸드 | 기타 식품 제조업 | 수산물(어묵,맛살)가공품 도매,원양수산업,수출입 |
| 2 | 082740 | HSD엔진 | 일반 목적용 기계 제조업 | 대형선박용엔진,내연발전엔진 |
| 3 | 001390 | KG케미칼 | 기초 화학물질 제조업 | 콘크리트혼화제, 비료, 친환경농자재, 수처리제 |
| 4 | 010060 | OCI | 기초 화학물질 제조업 | 타르제품,카본블랙,무수프탈산,농약원제,석탄화학제품,정밀화학제품,플라스틱창호재 제조,판매 |
모든 종목을 고려하면 좋지만, 임시로 10개 종목만 분석하였다.
시작일과 종료일은 5개년 데이터를 사용했다.
n = 10 # 생성할 종목수 지정
df_krx_list = df_krx['Symbol'].head(n*2) # 임시로 2배까지 루프
# 코스피 종목 추출
# 용도 : DataReader 사용시 종목별 기간 조회 건수가 상이하다.
# 코스피 데이터 날짜를 기준으로 가져오기 위해 사용
strt_dt = '2014-01-01' # 시작일 지정
end_dt = '2018-12-31' # 종료일 지정
kospi_df = fdr.DataReader('KS11', strt_dt,end_dt)
kospi_df.reset_index(inplace = True)
kospi_df.head()
| Date | Close | Open | High | Low | Volume | Change | |
|---|---|---|---|---|---|---|---|
| 0 | 2014-01-02 | 1967.19 | 2013.11 | 2013.89 | 1967.19 | 207770000.0 | -0.0220 |
| 1 | 2014-01-03 | 1946.14 | 1963.72 | 1964.63 | 1936.15 | 188530000.0 | -0.0107 |
| 2 | 2014-01-06 | 1953.28 | 1947.62 | 1961.85 | 1943.74 | 193630000.0 | 0.0037 |
| 3 | 2014-01-07 | 1959.44 | 1947.65 | 1965.74 | 1947.08 | 193030000.0 | 0.0032 |
| 4 | 2014-01-08 | 1958.96 | 1965.50 | 1966.95 | 1950.02 | 217070000.0 | -0.0002 |
stock_df = pd.DataFrame()
stock_df['Date'] = kospi_df['Date']
print("동기간 KOSPI 생성일수 : ", len(kospi_df['Date']))
normal_cnt = 0
err_cnt = 0
for code in df_krx_list:
stock = df_krx[df_krx.Symbol == code]
code_nm = list(stock.Name)[0]
try:
temp = fdr.DataReader(code, strt_dt, end_dt)
# 데이터일수가 시장보다 작으면 skip(최근 상장 데이터로 판단)
if len(temp) < len(kospi_df['Date']):
err_cnt += 1
print("skip : (",err_cnt,")", code, code_nm, strt_dt, end_dt, ", 건수 : ", len(temp))
continue
temp.reset_index(inplace = True)
temp_df = pd.merge(temp[['Date','Close']], kospi_df[['Date']], on='Date', how='right')
stock_df[code_nm] = temp_df.Close
normal_cnt += 1
print("정상 : (",normal_cnt,")", code, code_nm, strt_dt, end_dt, ", 건수 : ", len(temp), "->", len(stock_df))
except:
err_cnt += 1
print("skip : (",err_cnt,")", code, code_nm, strt_dt, end_dt, ", 건수 : ", len(temp))
if normal_cnt == n:
print('총', n,'개 생성 설정 / ', normal_cnt, '개 생성 완료')
break # n개 종목 생성시 종료
동기간 KOSPI 생성일수 : 1226
정상 : ( 1 ) 001040 CJ 2014-01-01 2018-12-31 , 건수 : 1331 -> 1226
정상 : ( 2 ) 011150 CJ씨푸드 2014-01-01 2018-12-31 , 건수 : 1298 -> 1226
정상 : ( 3 ) 082740 HSD엔진 2014-01-01 2018-12-31 , 건수 : 1305 -> 1226
정상 : ( 4 ) 001390 KG케미칼 2014-01-01 2018-12-31 , 건수 : 1313 -> 1226
정상 : ( 5 ) 010060 OCI 2014-01-01 2018-12-31 , 건수 : 1434 -> 1226
정상 : ( 6 ) 002360 SH에너지화학 2014-01-01 2018-12-31 , 건수 : 1410 -> 1226
정상 : ( 7 ) 001740 SK네트웍스 2014-01-01 2018-12-31 , 건수 : 1395 -> 1226
skip : ( 1 ) 285130 SK케미칼 2014-01-01 2018-12-31 , 건수 : 264
skip : ( 2 ) 011810 STX 2014-01-01 2018-12-31 , 건수 : 916
정상 : ( 8 ) 024070 WISCOM 2014-01-01 2018-12-31 , 건수 : 1233 -> 1226
정상 : ( 9 ) 011420 갤럭시아에스엠 2014-01-01 2018-12-31 , 건수 : 1298 -> 1226
skip : ( 3 ) 267290 경동도시가스 2014-01-01 2018-12-31 , 건수 : 402
정상 : ( 10 ) 002240 고려제강 2014-01-01 2018-12-31 , 건수 : 1258 -> 1226
총 10 개 생성 설정 / 10 개 생성 완료
생성된 종목별 종가데이터이다.
stock_df.head()
| Date | CJ | CJ씨푸드 | HSD엔진 | KG케미칼 | OCI | SH에너지화학 | SK네트웍스 | WISCOM | 갤럭시아에스엠 | 고려제강 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2014-01-02 | 117500 | 2415 | 8480.0 | 16550 | 188500 | 720 | 7400 | 4925 | 1940 | 30666 |
| 1 | 2014-01-03 | 117000 | 2425 | 8270.0 | 17000 | 195000 | 737 | 7460 | 4900 | 1940 | 30332 |
| 2 | 2014-01-06 | 115500 | 2410 | 8220.0 | 17400 | 195000 | 745 | 7270 | 4900 | 1990 | 30166 |
| 3 | 2014-01-07 | 114500 | 2425 | 8370.0 | 17100 | 193000 | 742 | 7810 | 4895 | 2000 | 30332 |
| 4 | 2014-01-08 | 115500 | 2440 | 8320.0 | 16900 | 196500 | 752 | 7900 | 4850 | 2020 | 30416 |
2) 데이터 정비
편의를 위해 오름차순 정렬 및 인덱스를 설정하고, 있을지 모를 결측치를 전일자로 채운다. 공적분에 사용할 data는 종가 자체 데이터를 사용했다.
# 데이터 정렬
stock_df.sort_values('Date', ascending=True, inplace=True) # ascending=True 오름차순, False 내림차순
# 결측치 채우기
stock_df.fillna(method='ffill', inplace=True)
# 인덱스 설정
stock_df.set_index('Date', inplace=True)
data = stock_df
3) 공적분 함수
# p-value가 지정된 값보다 작은 pair 쌍을 반환한다.
def find_cointegrated_pairs(data):
n = data.shape[1]
score_matrix = np.zeros((n, n))
pvalue_matrix = np.ones((n, n))
keys = data.keys()
all_pairs = []
pairs = []
# result
stock1 = []
stock2 = []
pvalue_list = []
check_95 = []
check_98 = []
for i in range(n):
for j in range(i+1, n):
S1 = data[keys[i]]
S2 = data[keys[j]]
result = coint(S1, S2)
score = result[0]
pvalue = result[1]
score_matrix[i, j] = score
pvalue_matrix[i, j] = pvalue
if pvalue < 0.05:
pairs.append((keys[i], keys[j]))
check_95.append('Y')
else:
check_95.append('N')
if pvalue < 0.02:
check_98.append('Y')
else:
check_98.append('N')
# result
stock1.append(keys[i])
stock2.append(keys[j])
pvalue_list.append(pvalue)
pair_pvalue = pd.DataFrame()
pair_pvalue['s1'] = stock1
pair_pvalue['s2'] = stock2
pair_pvalue['pvalue'] = pvalue_list
pair_pvalue['check_95'] = check_95
pair_pvalue['check_98'] = check_98
pair_pvalue.sort_values('pvalue', ascending=True, inplace=True) # ascending=True 오름차순
return score_matrix, pvalue_matrix, pair_pvalue, pairs
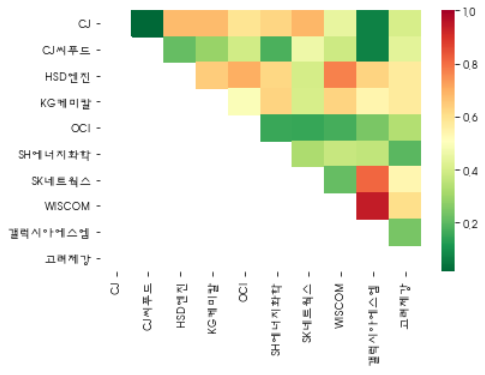
4) Heatmap 그래프
# Heatmap
instrumentIds = list(data.columns.values)
scores, pvalues, pair_pvalue, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds,
yticklabels=instrumentIds, cmap='RdYlGn_r',
mask = (pvalues >= 0.95))
plt.show()
# 유의한 pair 출력
print(pairs)
붉은색일수록 공적분관계가 유의한 것으로 판단되는 Pair이다.
Pair별 p-value 확인
pair_pvalue.head(5)
| s1 | s2 | pvalue | check_95 | check_98 |
|---|---|---|---|---|
| CJ | CJ씨푸드 | 0.015815 | Y | Y |
| CJ | 갤럭시아에스엠 | 0.071204 | N | N |
| CJ씨푸드 | 갤럭시아에스엠 | 0.071977 | N | N |
| OCI | SK네트웍스 | 0.153834 | N | N |
| OCI | SH에너지화학 | 0.155383 | N | N |
유의하게 판단되는 항목은 CJ, CJ씨푸드가 유일한 것으로 나타난다. 다만 10종목만 분석한 경우이므로, 종목 확장시 상당수의 Pair를 찾을 수 있을 것으로 보인다.
5) Pair 종목 시계열 비교
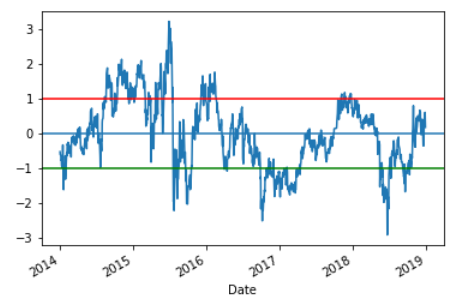
데이터를 파악해보기 위한 용도로 Z-score 그래프를 그려보자. 여기서 사용되는 Z-score는 일정한 크기를 부여하기 위한 용도로만 사용되었다. 만약, 실제 주식시장 분석 용도로 사용할 경우에는 정규분포를 가정하게 되므로 실제 비대칭적 주식시장에는 맞지 않아 유의해야 한다.
def zscore(series):
return (series - series.mean()) / np.std(series)
zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color='red')
plt.axhline(-1.0, color='green')
plt.show()
6) 트레이딩 전략
Step 1: Setup your problem
종목1의 주가를 S1, 종목2를 S2로 두고 아래와 같이 Ratio 비율을 계산한다.
Ratio = S1/S2 Ratio 비율은 S1 1개당 S2의 수량을 의미한다.
매수 신호(-1이하) 포착시, S1을 n개 매수하고, S2를 n * Ratio개 매도한다. 매도 신호(+1이상) 포착시, S1을 n개 매도하고, S2를 n * Ratio개 매수한다.
Step 2: Collect Reliable and Accurate Data
트레이딩 전략을 세울 Pair를 셋팅한다.
# 가장 유의성이 높은 2개 종목을 추출한다.
s1_nm = 'CJ'
s2_nm = 'CJ씨푸드'
S1 = data[s1_nm]
S2 = data[s2_nm]
Step 3: Split Data
검증을 위해 7:3 비율로 Train:Test 셋으로 나눈다.
ratios = S1 / S2
cut = int(len(ratios)*0.7)
train = ratios[:cut]
test = ratios[cut:]
S1_train = S1.iloc[:cut]
S2_train = S2.iloc[:cut]
S1_test = S1.iloc[cut:]
S2_test = S2.iloc[cut:]
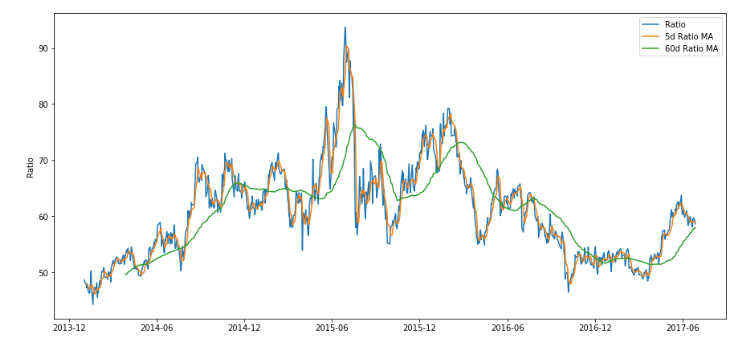
Step 4: Feature Engineering
다음과 같은 요소들에 의해 매도/매수 신호를 포착한다.
- 60 day Moving Average of Ratio: Measure of rolling mean
- 5 day Moving Average of Ratio: Measure of current value of mean
- 60 day Standard Deviation
- z score: (5d MA — 60d MA) /60d SD
ratios_mavg5 = train.rolling(window=5,
center=False).mean()
ratios_mavg60 = train.rolling(window=60,
center=False).mean()
std_60 = train.rolling(window=60,
center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()
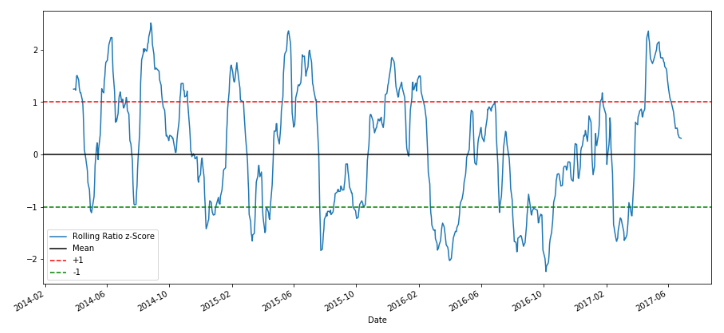
plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()
최근 5일 이평선과 60일 이평선(평균)으로 산출한 Z-score를 그래프로 확인해보자. 대부분 -1~1사이에 위치해 있으며 평균으로 회귀하려는 경향을 확인할 수 있다.
Step 5: Model Selection
Z-score가 -1이하로 떨어지면 S1매수&S2매도하고 +1이상 오르면 S1매도&S2매수한다.
Step 6: Train, Validate and Optimize
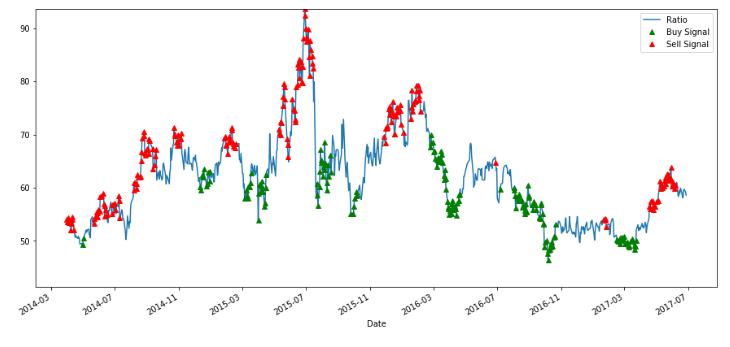
모델이 수행하는 액션을 그래프로 확인해보자.
# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color='g', linestyle='None', marker='^')
sell[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend(['Ratio', 'Buy Signal', 'Sell Signal'])
plt.show()
위 그래프는 Ratio에 대한 그래프이다.
다음 코드를 통해 실제 주가 그래프로 시그널을 확인할 수 있다.
다만, 두개 주가가 스케일 차이가 있을 수 있으므로 편의상 log처리 후 그래프로 나타냈다.
실제 모델에서는 단순 종가를 사용한다.
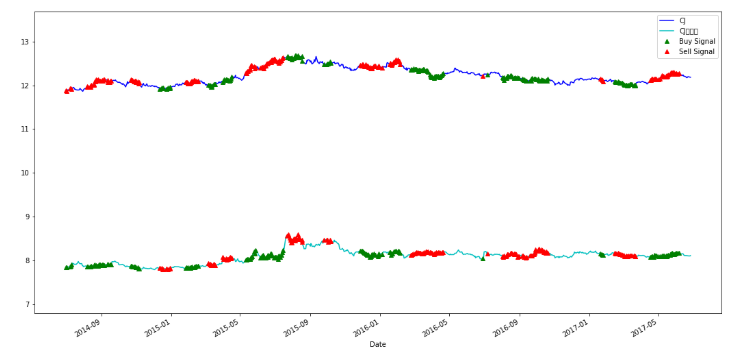
# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1_log = S1_train[60:].map(lambda x : np.log(x))
S2_log = S2_train[60:].map(lambda x : np.log(x))
S1_log[60:].plot(color='b')
S2_log[60:].plot(color='c')
buyR = 0*S1_log.copy()
sellR = 0*S1_log.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1_log[buy!=0]
sellR[buy!=0] = S2_log[buy!=0]
# When selling the ratio, sell S1 and buy S2
buyR[sell!=0] = S2_log[sell!=0]
sellR[sell!=0] = S1_log[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1_log.min(),S2_log.min())-1,max(S1_log.max(),S2_log.max())+1))
plt.legend([s1_nm, s2_nm, 'Buy Signal', 'Sell Signal'])
plt.show()
일정 간격을 유지하며 움직이고 있음을 보다 명확하게 확인할 수 있다.
실전 트레이딩 전략 짜기
원하는대로 액션을 수정해볼 수 있다. 셋팅된 기준은 Z-score를 기준으로
+1 이상일 경우 : S1 n개 매도, S2 n * ratio 매수
-1 이하일 경우 : S1 n개 매수, S2 n * ratio 매도
-0.5 ~ 0.5 사이이면서 현재 수익(+)을 내고 있을 경우, 포지션 정리하여 이익을 실현한다.
# Trade using a simple strategy
def trade(S1, S2, window1, window2):
# If window length is 0, algorithm doesn't make sense, so exit
if (window1 == 0) or (window2 == 0):
return 0
# Compute rolling mean and rolling standard deviation
ratios = S1/S2
ma1 = ratios.rolling(window=window1,
center=False).mean()
ma2 = ratios.rolling(window=window2,
center=False).mean()
std = ratios.rolling(window=window2,
center=False).std()
zscore = (ma1 - ma2)/std
# Simulate trading
# Start with no money and no positions
money = 0
countS1 = 0
countS2 = 0
for i in range(len(ratios)):
# Sell short if the z-score is > 1
if zscore[i] > 1:
money += S1[i] - S2[i] * ratios[i]
countS1 -= 1
countS2 += ratios[i]
print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
# Buy long if the z-score is < 1
elif zscore[i] < -1:
money -= S1[i] - S2[i] * ratios[i]
countS1 += 1
countS2 -= ratios[i]
print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
# Clear positions if the z-score between -.5 and .5
# -0.5~0.5 사이인 경우 수익일 경우 이익 실현
elif abs(zscore[i]) < 0.5 and (money + S1[i] * countS1 + S2[i] * countS2) > 0 :
money += S1[i] * countS1 + S2[i] * countS2
countS1 = 0
countS2 = 0
print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
return money
아래 코드로 시뮬레이션 해보자.
money = trade(S1_train, S2_train, 78, 5)
money
65149.11의 이익을 창출할 것으로 예상된다.
Step 7: Backtest on Test Data
Test데이터로 백테스팅을 해보자.
money = trade(S1_test, S2_test, 78, 5)
money
576053.30의 이익이 산출되었다.
함수에서 설정한 78과 5는 window 크기, 즉 평균치로 볼 기간과 현재시점으로 볼 일수를 의미한다.
78이라는 숫자는 어떻게 나왔을까?
최적의 숫자를 설정하기 위해 그리드서치를 수행해볼 수 있다.
실제로 78은 예제 데이터를 기준으로 그리드서치한 결과이다.
Window Size Search
# train
length_scores = [trade(S1_train,
S2_train, l, 5)
for l in range(120)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)
# Test
length_scores2 = [trade(S1_test,
S2_test,l,5)
for l in range(120)]
print (best_length, 'day window:', length_scores2[best_length])
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])
plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()
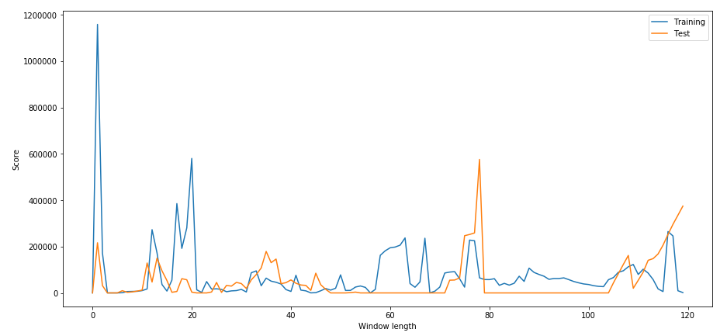
그래프는 Train과 Test 데이터의 Window일수별 수익금액 시뮬레이션 결과이다.
둘다 높은 수익을 낼 것으로 예상되는 구간을 찾아야 한다.
해당 데이터에서는 75~80 사이가 비교적 합리적일 것으로 판단된다.
Reference
https://medium.com/auquan/pairs-trading-data-science-7dbedafcfe5a
https://m.blog.naver.com/PostView.nhn?blogId=chunjein&logNo=100201888073&proxyReferer=https%3A%2F%2Fwww.google.co.kr%2F