* 본 포스트는 개인연구/학습 기록 용도로 작성되고 있습니다.

[Python] Kalman Filter를 활용한 Pair Trading

By MK on January 20, 2019

터널을 통과하는 차의 GPS 신호가 사라졌다. 터널안의 차를 어떻게 탐색할 수 있을까?

발사된 미사일을 격추시키기 위해 미래 미사일의 위치를 어떻게 추정할 수 있을까?

칼만필터는 공간선형모델로 주로, 네비게이션에서 위치를 추적하는데 쓰이거나 미사일 위치를 추적하는 등 관측치를 기반으로 현재의 상태를 예측하는데 활용되는 모델이다.

비교적 빠르고 쉽게 구현할 수 있으며 특정 조건에서 정상적으로 분산된 센서의 잡음에 대한 최적 추정값을 제공한다.

실제로 NASA에서 활용하여 아폴로호에서 달 착륙시 사용되기도 했다.

이에 따라 경제학 분야에서도 랜덤하게 변화는 상태에서 가장 가능성이 높은 예측 상태를 추정하기 위해 활용되었는데 환율예측이나 주가예측 등 다양한 연구사례들이 있다.

현재는 인공지능의 발달로 RNN과 대조되어 사용되기도 하지만, 각각의 특장점이 있어 여전히 많이 쓰이고 있는 칼만 필터에 대해 인지하고 넘어가야할 필요가 있다.

칼만필터는 연산을 최적으로 수행하기 위해 강력한 매개변수값이 필요하다. 이는 정규분포에 근거한다는 단점이 있다.

칼만필터는 움직이고 있는 관측치를 정보를 활용해 최적의 예측값을 만들어낸다.

즉, 상태예측과 측정값을 업데이트 해나가는 과정을 반복 수행한다.

실제 판독결과와 비교하여 예측치와 근사하면 그 위치값에 대한 확신을 강화하고 예상이 벗어나면 가중치를 낮추며 정확도를 높여나간다.

칼만필터를 알아보기 전에 선형 회귀 방정식을 살펴보자

a_k = βb_k + α

여기서 a~k~와 b~k~는 두 종목의 종가이고 β와 α는 기울기(Slope)와 절편(Intercept)이다. 벡터 형태로 표현하면 아래와 같다.

a_k = βb_k

β = [β α]

b_k = [b_k1]

칼만 필터는 잡음이 있는 데이터스트림에서 재귀적으로 작동해 통계적 최적추정치를 산출하는 모델이다.

칼만필터의 상태공간 모델의 방정식은 다음과 같다.

x_k+1 = A_kx_k + w_k

z_k = H_kx_k + v_k

x_k 와 z_k 는 시각 k에서 숨겨진 상태와 관측 벡터이다.

A_k 와 H_k 는 전이행렬(일종의 함수)를 의미한다.

w_k 와 v_k 는 평균이 0인 가우시안 잡음이다.

관측치를 기반으로 얻는 주가의 조정 종가를 z_k 라 할때 측정행렬 H는 마감가격과 조정마감가격으로 구성된 1X2 벡터이다. 이 자체가 단순히 두 Asset 사이에서의 선형 회귀이다.

이를 응용하여 숨겨진 상태변수 x_k 가 β로 표시된 선형회귀로 이루어진다고 가정한다. 또한 행렬 A를 랜덤워크로 가정하여 아래와 같은 산식으로 재구성한다.

β_k+1 = Iβ_k + w_k

다시 말해 다음 스텝을 위한 β는 현재의 β와 약간의 잡음을 포함하는 개념이다.

I는 단위행렬로 칼만 방정식을 단순화하는 역할을 하게 된다.

이제 칼만필터의 관측 방적식을 통해 2개의 주가의 spread를 분석해보자!

1. 데이터 가져오기

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import pandas as pd
import numpy as np
from pykalman import KalmanFilter
import statsmodels
import statsmodels.api as sm

KRX에서 제공하는 MarketData를 통해 5개년 종목 시세를 CSV로 저장해 두었다.

http://marketdata.krx.co.kr/mdi#document=13020101

data_all = pd.read_csv('./datas/data_all.csv')
tickers = ['Shinhan', 'KB']

# 인덱스 설정
data_all.set_index('Date', inplace=True)

# 데이터 정렬
data_all.sort_values('Date', ascending=True, inplace=True) # ascending=True 오름차순, False 내림차순

2. 종목 살펴보기

주가 추이 그래프

data_all.plot()

img_area

3. 데이터 파악하기

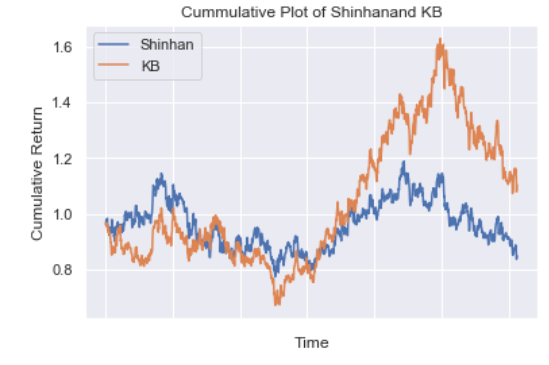
누적 수익률 그래프 pct_change는 pandas에서 제공하는 변화률 계산 함수이다.

cumm_rtn = (1 + data_all.pct_change()).cumprod()  # 일일수익률 누적곱
cumm_rtn.plot();
plt.ylabel('Cumulative Return');
plt.xlabel('Time');
title = 'Cummulative Plot of ' + tickers[0] + 'and ' + tickers[1]
plt.title(title);

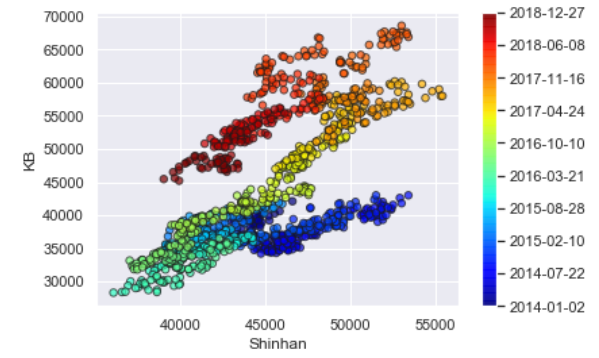
img_area

두 종목의 종가 비교 그래프

colors = np.linspace(0.1, 1, len(data_all))
sc = plt.scatter(data_all[tickers[0]], data_all[tickers[1]], s=30,
                 c=colors, cmap=plt.get_cmap('jet'), edgecolor='k', alpha=0.7)
cb = plt.colorbar(sc)
cb.ax.set_yticklabels([p for p in data_all[::len(data_all)//9].index])
plt.xlabel(tickers[0])
plt.ylabel(tickers[1])

img_area

4. Kalman Filter

obs_mat = sm.add_constant(data_all[tickers[0]].values, prepend=False)[:, np.newaxis]
delta = 1e-5
trans_cov = delta / (1 - delta) * np.eye(2)

# y is 1-dimensional, (alpha, beta) is 2-dimensional
kf = KalmanFilter(n_dim_obs=1, n_dim_state=2,
                  initial_state_mean=np.zeros(2),
                  initial_state_covariance=np.ones((2, 2)),
                  transition_matrices=np.eye(2),
                  observation_matrices=obs_mat,
                  observation_covariance=1.0,
                  transition_covariance=trans_cov)

상대 비교할 종목의 가격추이로 상태 평균과 분산을 측정한다.

state_means, state_covs = kf.filter(data_all[tickers[1]])

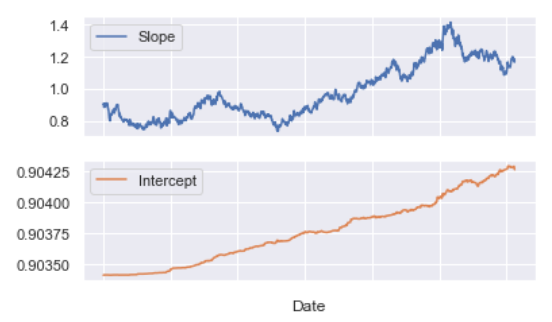
칼만필터 베타 확인

beta_kf.plot(subplots=True);

img_area

다음 상태를 예측하는데 사용하는 β의 Slope는 증가 후 유지하는 수준, Intercept는 지속 증가하는 추세이다.

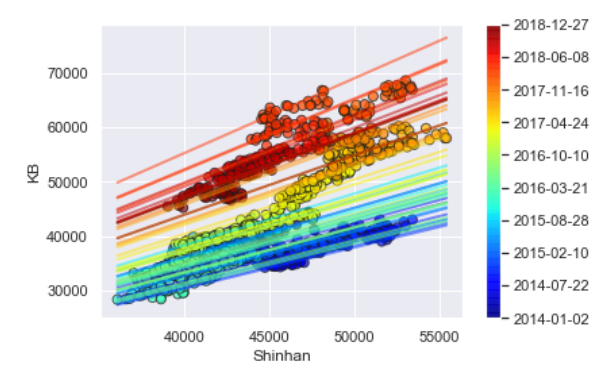
칼만필터 그래프

# visualize the correlation between assest prices over time
dates = [p for p in data_all[::int(len(data_all)/10)].index] # str(p.date())
colors = np.linspace(0.1, 1, len(data_all))
sc = plt.scatter(data_all[tickers[0]], data_all[tickers[1]],
                 s=50, c=colors, cmap=plt.get_cmap('jet'), edgecolor='k', alpha=0.7)
cb = plt.colorbar(sc)
cb.ax.set_yticklabels([p for p in data_all[::len(data_all)//9].index]); # [str(p.date())
plt.xlabel(tickers[0])
plt.ylabel(tickers[1])

# add regression lines
step = 25
xi = np.linspace(data_all[tickers[0]].min(), data_all[tickers[0]].max(), 2)
colors_l = np.linspace(0.1, 1, len(state_means[::step]))
for i, b in enumerate(state_means[::step]):
    plt.plot(xi, b[0] * xi + b[1], alpha=.5, lw=2, c=plt.get_cmap('jet')(colors_l[i]))

파란색 값들은 과거, 붉은 색 값들이 최근 데이터이다.

회귀선이 시간에 따라 조정되는 현상을 시각적으로 나타낼 수 있다.

그래프에 따르면 Intercept가 증가하여 격차가 벌어지고 있는 걸 확인할 수 있다.

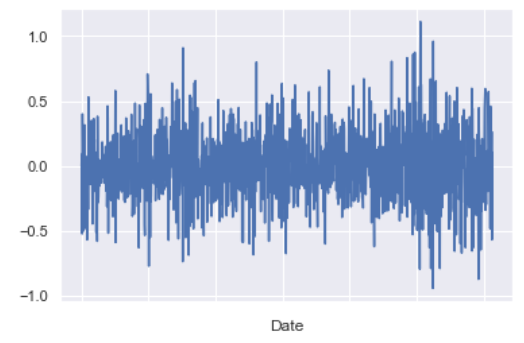
img_area

5. Spread

spread_kf = data_all[tickers[1]] - data_all[tickers[0]] * beta_kf['Slope'] - beta_kf['Intercept']
spread_kf.plot();

img_area

Reference

http://www.thealgoengineer.com/2014/online_linear_regression_kalman_filter/

https://towardsdatascience.com/kalman-filter-an-algorithm-for-making-sense-from-the-insights-of-various-sensors-fused-together-ddf67597f35e

시계열분석