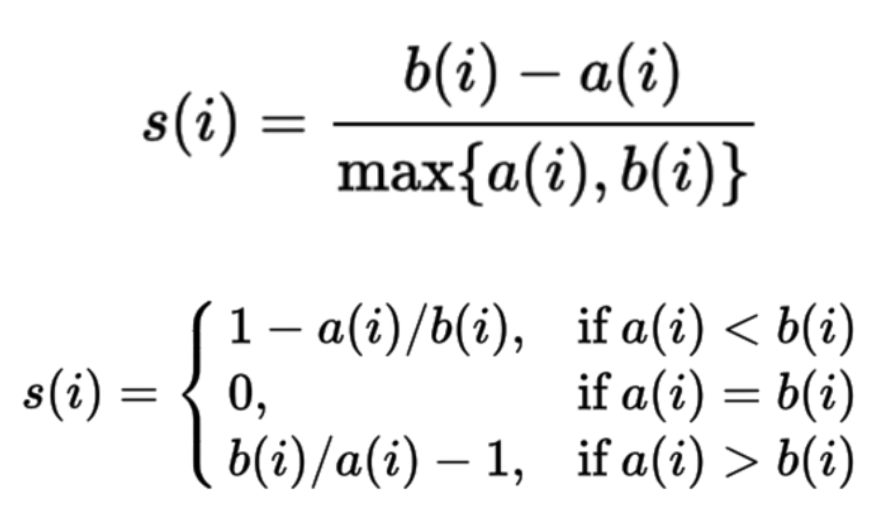* 본 포스트는 개인연구/학습 기록 용도로 작성되고 있습니다.
[Python] K-means를 통한 기업 패턴 분류
By MK on January 9, 2019
4차산업혁명 시대에 이르면서 기업마다 다양한 디지털 산업을 영위하고, 디지털업계가 유통업, 금융업에 진출하면서 산업의 경계가 허물어져 가고 있다.
점점 기존의 산업분류체계에 대한 의구심을 갖고 새로운 기업 패턴 분류에 대한 니즈가 생겨나게 되었다.
이러한 관점에서 가장 눈에 띈 시도를 한 기업이 켄쇼이다. 켄쇼는 기업의 패턴분석을 통해 4차산업혁명 기업들을 분류하고 인덱스를 만들어 관리하였다.
이러한 산업 트렌드 변화의 출발선에서 가장 기본적인 기업데이터를 가지고 패턴분석해보고자 한다.
데이터 분류는 임의로 5개로 분류하였다.
1. 데이터 가져오기
산업정보를 제외하고 해당 기업의 정보만으로 구성된 순수 기업 데이터 를 pickle 변수로 생성해 두었다.
corp_features은 freature데이터들만으로 구성된 데이터이다.
import pickle
import pandas as pd
import numpy as np
with open('./pickles/dataset.p', 'rb') as file:
data = pickle.load(file)
corp_features = pickle.load(file)
2. 데이터 스케일링
모델링 전에는 항상 스케일링을 체크해준다. 여기서는 min/max 스케일링법을 사용하였다.
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
scaler.fit_transform(corp_features)
feature = scaler.fit_transform(corp_features)
3. 하이퍼파라메터 설정
몇개의 클러스터로 분류할지 하이퍼파라메터는 아래 코드로 찾을 수 있다.
elbow기법
def elbow(X):
sse = []
for i in range(1,11):
km = KMeans(n_clusters=i,algorithm='auto', random_state=42)
km.fit(X)
sse.append(km.inertia_)
plt.plot(range(1,11), sse, marker='o')
plt.xlabel('K')
plt.ylabel('SSE')
plt.show()
elbow(feature)
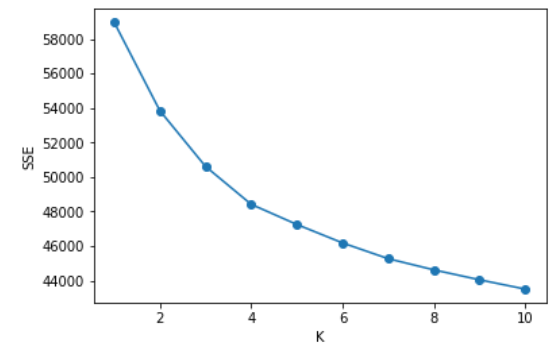
서로 다른 K개 클러스터 분류의 오차제곱값(SSE)를 확인할 수 있다. 변곡점이 되는 지점에서 K값을 결정하면 된다. 샘플 데이터의 경우 뚜렷하진 않지만 대략 4 언저리에서 elbow를 형성하는 것을 확인할 수 있다.
실루엣 기법
실루엣 계수는 한 클러스터 안에 데이터들이 다른 클러스터와 비교해서 얼마나 비슷한가를 나타낸다.
클러스터 안의 거리가 짧을수록 좋고(cohesion), 다른 클러스터와의 거리가 멀수록 좋다.(separation)
실루엣은 -1~1사이의 값을 가지며 1에 가까울수록 잘 부합하는 데이터이다. 실루엣 계수가 0이면 지금클러스터나 다른 클러스터 어디에 있든 상관 없음을 의미한다.
# 실루엣 기법
import numpy as np
from sklearn.metrics import silhouette_samples
from sklearn.datasets import make_blobs
from matplotlib import cm
def plotSilhouette(X, y_km):
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric = 'euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(i/n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0,
edgecolor='none', color=color)
yticks.append((y_ax_lower + y_ax_upper)/2)
y_ax_lower += len(c_silhouette_vals)
silhoutte_avg = np.mean(silhouette_vals)
plt.axvline(silhoutte_avg, color = 'red', linestyle='--')
plt.yticks(yticks, cluster_labels+1)
plt.ylabel('K')
plt.xlabel('실루엣 계수')
plt.show()
k= 4
X, y = make_blobs(n_samples=150, n_features=2, centers=3, cluster_std=0.5,
shuffle=True, random_state=0)
km = KMeans(n_clusters=k, algorithm='auto', random_state=42)
y_km = km.fit_predict(feature)
plotSilhouette(feature, y_km)
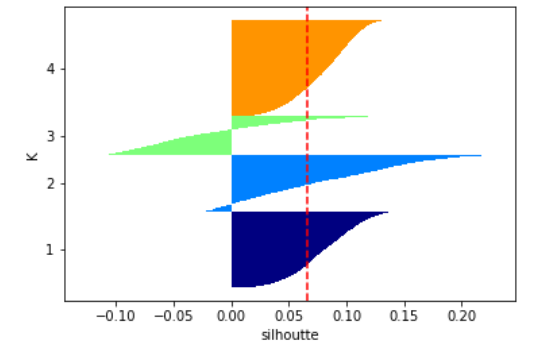
결과를 보면 유의하지 않은 데이터가 많은 것으로 보인다.
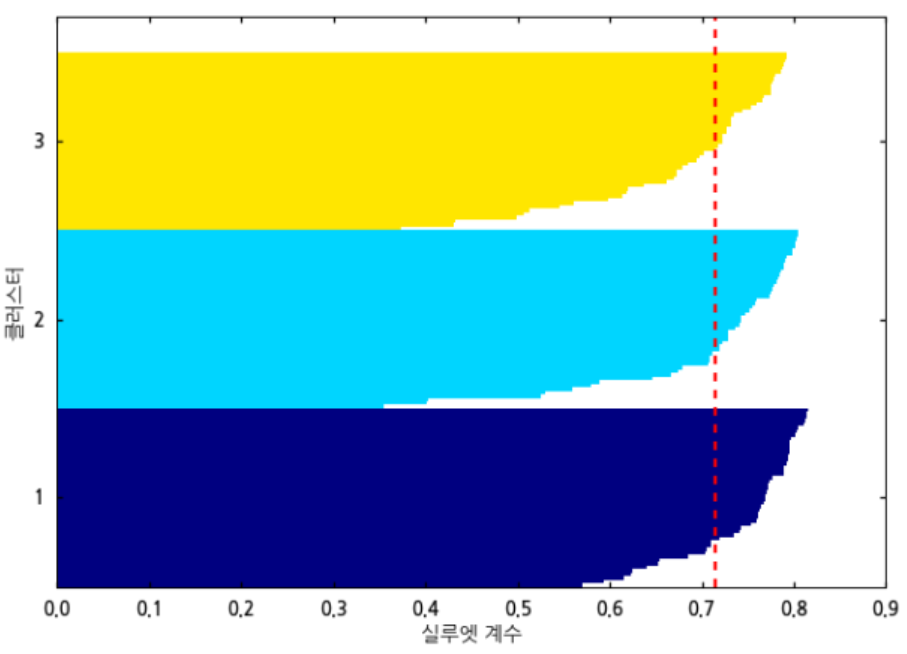
이상적인 그림은 아래와 같다.
이 예는 코드에 실제로 사용한 데이터의 결과는 아니다. 분류에 의미있는 데이터를 넣었을때 이상적인 결과 그래프는 이처럼 0에 가까운 데이터가 많지 않고 평균이 1에 가까울수록 좋다.
즉, 예시로 사용된 결과는 크게 유의하다고 보긴 어려울 것 같다. 그럼에도 불구하고 코드의 활용 및 기록을 위해서 다음 단계까지 진행해보자.
4. K-means 모델실행
n_clusters 파라메터를 통해 분류 class수를 결정할 수 있다.
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
k = 4
# create model and prediction
model = KMeans(n_clusters=k,algorithm='auto')
model.fit(feature)
predict = pd.DataFrame(model.predict(feature))
predict.columns=['predict']
5. 예측결과 합치기
# 결과 합치기
final_df = pd.DataFrame(np.hstack((predict, feature)))
# 컬럼명 지정
cols = list(corp_features.columns.values)
cols.insert(0,'group')
final_df.columns = cols
참고로 생성한 결과 그룹의 값을 0~숫자가 아닌, 지정값으로 변경할 수도 있다. 여기서는 plot그래프를 그릴 예정이므로 사용하진 않았다.
# 숫자 to 그룹명 변경
group_name = {0: 'gr01',
1: 'gr02',
2: 'gr03',
3: 'gr04'
final_df['group'] = final_df['group'].replace(group_name)
6. 결과 시각화 확인(t-SNE활용)
데이터의 분류를 시각화해서 확인하고 싶으나, 다차원의 데이터를 눈으로 확인하기란 불가능에 가깝다. 단, 차원을 줄이면 가능하다. 차원을 축소하여 feature를 2,3로 줄인 후 그래프를 그려 확인해볼 수 있다.
주로 PCA, tSNE기법을 많이 사용하고 있다. 여기서는 tSNE 코드를 사용하였다.
먼저 생성된 결과를 데이터 프레임으로 변환한다.
feature_df = pd.DataFrame(feature)
차원축소
import numpy as np
from sklearn.manifold import TSNE
# 2개의 차원으로 축소
transformed = TSNE(n_components=2).fit_transform(feature_df)
transformed.shape
시각화
xs = transformed[:,0]
ys = transformed[:,1]
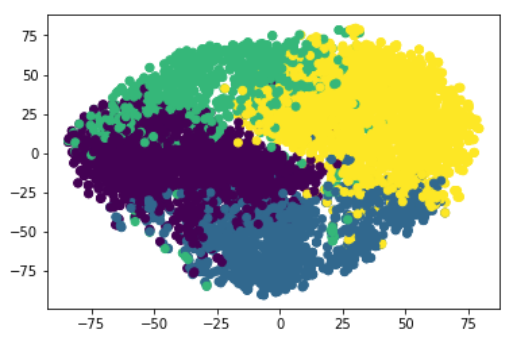
plt.scatter(xs,ys, c=final_df['group']) #라벨은 색상으로 분류됨
plt.show()
결과를 확인해보면 상당부분 노란색 영역에 분포하지만 어느정도 5개 분류가 명확한 것을 확인할 수 있다. 향후 데이터 특징 분석을 통해 분류된 기업들간에 어떤 패턴이 있는지 확인해보면 의미있는 데이터를 얻을 수도 있을 것이다.
어느정도 분류가 잘 되는 것처럼 보이지만 3번의 실루엣 계수 결과를 통해 평가해보면 크게 유의하지 않은 분류의 데이터가 많아 사용할 수 없다고 판단된다.
Reference
http://blog.naver.com/PostView.nhn?blogId=samsjang&logNo=221017639342&categoryNo=87&parentCategoryNo=49&viewDate=¤tPage=1&postListTopCurrentPage=1&from=postView http://astralworld58.tistory.com/59